Introduction
The dividend discount model, also known as the Gordon Growth Model, is used to determine a stock’s intrinsic value based on a future series of dividends that grow at a constant rate. It is a popular and straightforward variant of the dividend discount model (DDM). This method disregards current market conditions. Companies belonging to a diverse set of industries can be compared and analyzed irrespective of the current market conditions using this simplified model while considering dividend pay-out factors and the expected returns in the market, in this way, the Gordon Growth Model provides an untainted picture of the stock.
In-Depth Analysis
The Gordon Growth Model functions on an assumption of constant growth to calculate the value of a company’s stock based on payments or dividends it pays to the common equity holders of the stock. The three critical elements in the model are dividends per share (DPS), the growth rate in dividends per share, and the required rate of return (RoR).
Dividend per share is the amount paid by the company to its stockholders per stock annually based on the number of stocks they own. The growth rate in dividends per share is the rate of increase of dividend paid per share from one year to the next. The required rate of return is the minimum rate of return acceptable by investors interested in buying a specific company’s stocks. There are multiple models of investors who use this model to estimate the rate.
GGM works on the assumption that the company has existed infinitely and pays dividends per share that increase at a constant rate. To analyze the value of a single stock, the Gordon Growth model takes the infinite series of dividends per share and discounts them back into the present using the required rate of return.
Underlying Assumptions
The Gordon Growth Model assumes the following conditions:
- The company’s business model is stable; i.e., there are no significant changes in its operations.
- The company grows at a constant, unchanging rate.
- The company has stable financial leverage.
- The company’s free cash flow is paid as dividends.
Gordon Growth Method Formula
Three variables are included in the Gordon Growth Model formula: (1) D1 or the expected annual dividend per share for the following year, (2) k or the required rate of return, and (3) g or the expected dividend growth rate. With these variables, the value of the stock can be computed as:
Intrinsic Value = D1 / (k – g)
To illustrate, take a look at the following example: Company A’s is listed at $40 per share. Furthermore, Company A requires a rate of return of 10%. Company A pays dividends of $2 per share for the following year, which investors expect to grow 4% annually. Thus, the stock value can be computed:
Intrinsic Value = 2 / (0.1 – 0.04)
Intrinsic Value = $33.33
This result indicates that Company A’s stock is overvalued since the model suggests that the stock is only worth $33.33 per share.
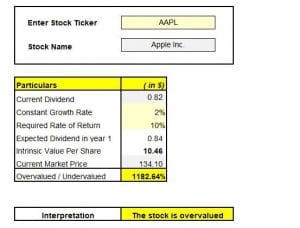
Using a MarketXLS Template
Using a MarketXLS Template
To work out the evaluation process in excel, one of the handiest things to use is the MarketXLS template for Gordon Growth Model. It works in two simple steps:
Step 1: Enter the stock ticker in your MarketXLS enabled MS Excel software.
Step 2: Compare the output against as many potential stocks as you want and save your results for better decision-making.
Link to the template: https://www.marketxlswp.com/template/dividend-growth-model-gordon-method/
Drawbacks
The Gordon Growth Model functions on the assumption of constant growth, which results in its biggest shortcoming. This model ignores some of the realistic possibilities on which a company’s stock can sometimes fail to perform. It’s a rarity to see a constant growth in the dividend per share paid by a company due to unplanned financial burdens, inability to generate profit, etc. Another major limitation is the relationship between the discount factor and the growth rate used in the model. If the required rate of return is less than the growth rate of dividends per share, the result is a negative value, making the model pointless. If the required rate of return is the same as the growth rate, the value per share approaches infinity.
Disclaimer
None of the content published on marketxls.com constitutes a recommendation that any particular security, portfolio of securities, transaction, or investment strategy is suitable for any specific person.
The author is not offering any professional advice of any kind. The reader should consult a professional financial advisor to determine their suitability for any strategies discussed herein.
The article is written to help users collect the required information from various sources deemed authority in their content. The images, copyrights, and trademarks, if any, are the property of their owners, and no other representations are made.
References
https://corporatefinanceinstitute.com/