The Portfolio Optimization with MarketXLS calculates the optimal capital weightings for a basket of investments that gives the highest return for the least risk. The MarketXLS add-in enables it to be applied to either financial instrument or business portfolios. The ability to apply optimization analysis to a portfolio represents an excellent framework for driving capital allocation and investment.
What Is Portfolio Optimization?
Portfolio optimization is called as ‘optimal asset allocation’, building the portfolio to yield the maximum possible return while maintaining the amount of risk you’re willing to carry. Creating a balanced portfolio means you want to spread your investment capital across various assets. Then, you can balance those assets to attain your desired risk-reward outcome.
Portfolio optimization should result in what investors call an ‘efficient portfolio’. This means it’s generating the highest possible return at your established risk tolerance. Alternatively, this term may refer to a portfolio with the minimum amount of risk for the return it seeks, although it’s less common usage.
Advantages of Portfolio Optimization
Maximizing Return – The first and foremost objective of portfolio optimization is maximizing return for a given risk level. The risk-return is maximized at the point on the efficient frontier that represents the optimal portfolio. So investors pursuing the process of portfolio optimization are often able to achieve high returns per unit of risk for their portfolio.
Diversification – Optimal Portfolios are well diversified to do away with the unsystematic risk or the non-priced risk. Diversification helps in protecting investors against downside in case a particular asset under-performs. The other assets in the portfolio will protect the investor’s portfolio from crashing.
Key features of the Portfolio Optimization with MarketXLS
1. Ease and flexibility of input, with embedded help, prompt.
2. Ability to specify the weights held in each asset in the portfolio.
3. Specifies the returns and the risk associated using MarketXLS formula for the optimized portfolio.
4. Optimization can be made on the Sharpe ratio or Sortino ratio as well as to get return-risk ratio.
5. Results are saved for both minimum and maximum levels of returns and risk with Value-at-risk (VaR) calculation for that resulting portfolio.
6. The intuitive graphical result is displayed with the Monte Carlo simulation and Efficient Frontier, including probability analysis on a specified portfolio.
Process of Portfolio Optimization with MarketXLS
Portfolio Optimization with MarketXLS® add-in helps investors assess their portfolios and make investment decisions. MarketXLS® template has now made it easy to perform Portfolio Optimization with just a few clicks. The asset allocation for an optimal portfolio is essentially a two-part process:
1. Selecting asset and respective weights – Portfolio managers first choose the asset classes they want to allocate funds. Then they decide the weight of every asset class is included.
2. Selecting the Function – After deciding the asset classes, the investor decides how much of a particular stock or a bond he wants to include in the portfolio based on the highest returns and minimal returns using MarketXLS.
The MarketXLS provides formulas for Sharpe Ratio, Sortino Ratio, Value-at-risk(VaR), Efficient Frontier, Monte Carlo, Portfolio Beta, Weighted index to optimize the portfolio representing the risk-return relationship.
Input:
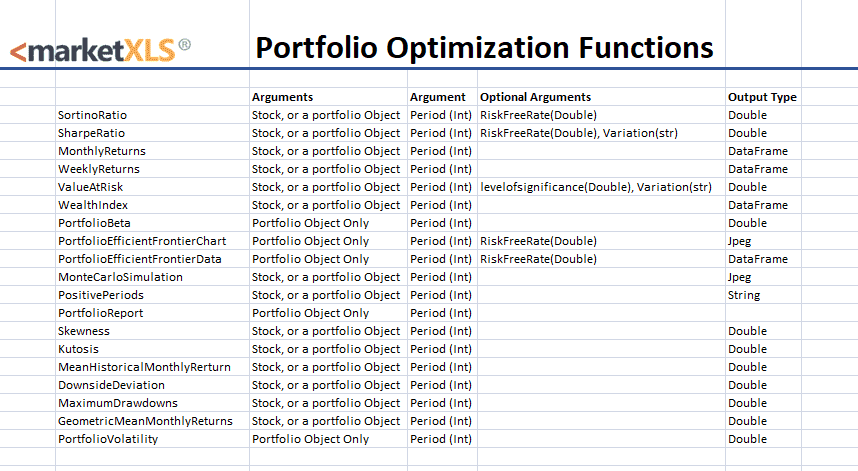
Output:
Here are some of the outputs of graphs provided in MarketXLS tool:
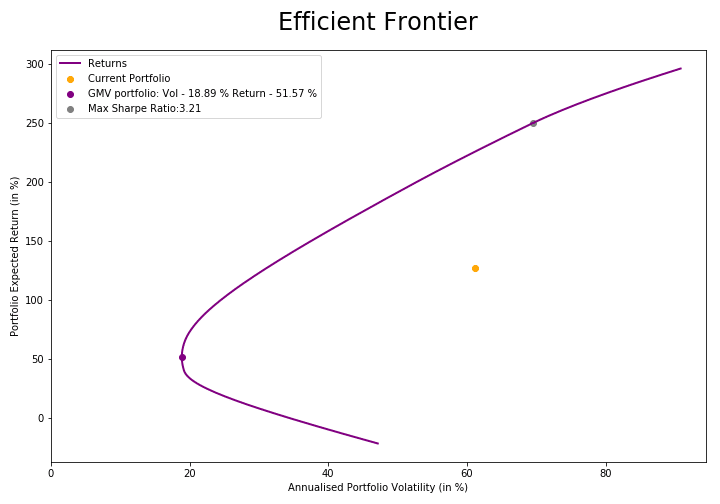
The Efficient Frontier gives a combination of assets with the optimal level of expected return for a given level of risk, all the portfolios on the line are efficient.
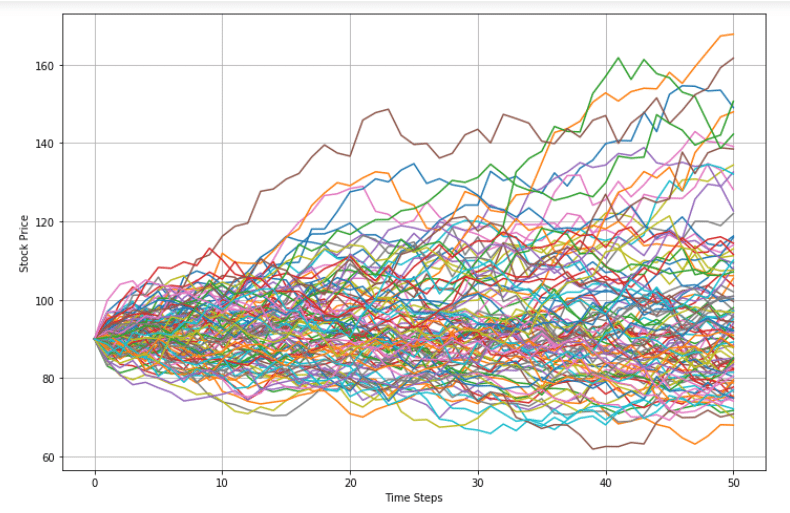
Monte Carlo simulates the stock price with 100 repeated simulations of random number with time steps on the graph:
Portfolio Optimization with MarketXLS is efficient for those investors who want to maximize the risk-return since this process is targeted at maximizing the return for every additional unit of risk taken in the portfolio. The investors can combine a combination of risky assets with a risk-free asset. Portfolio Optimization gives the portfolio that would generate the highest possible return from the combination.







