Trading Using The Fibonacci Retracement Strategy
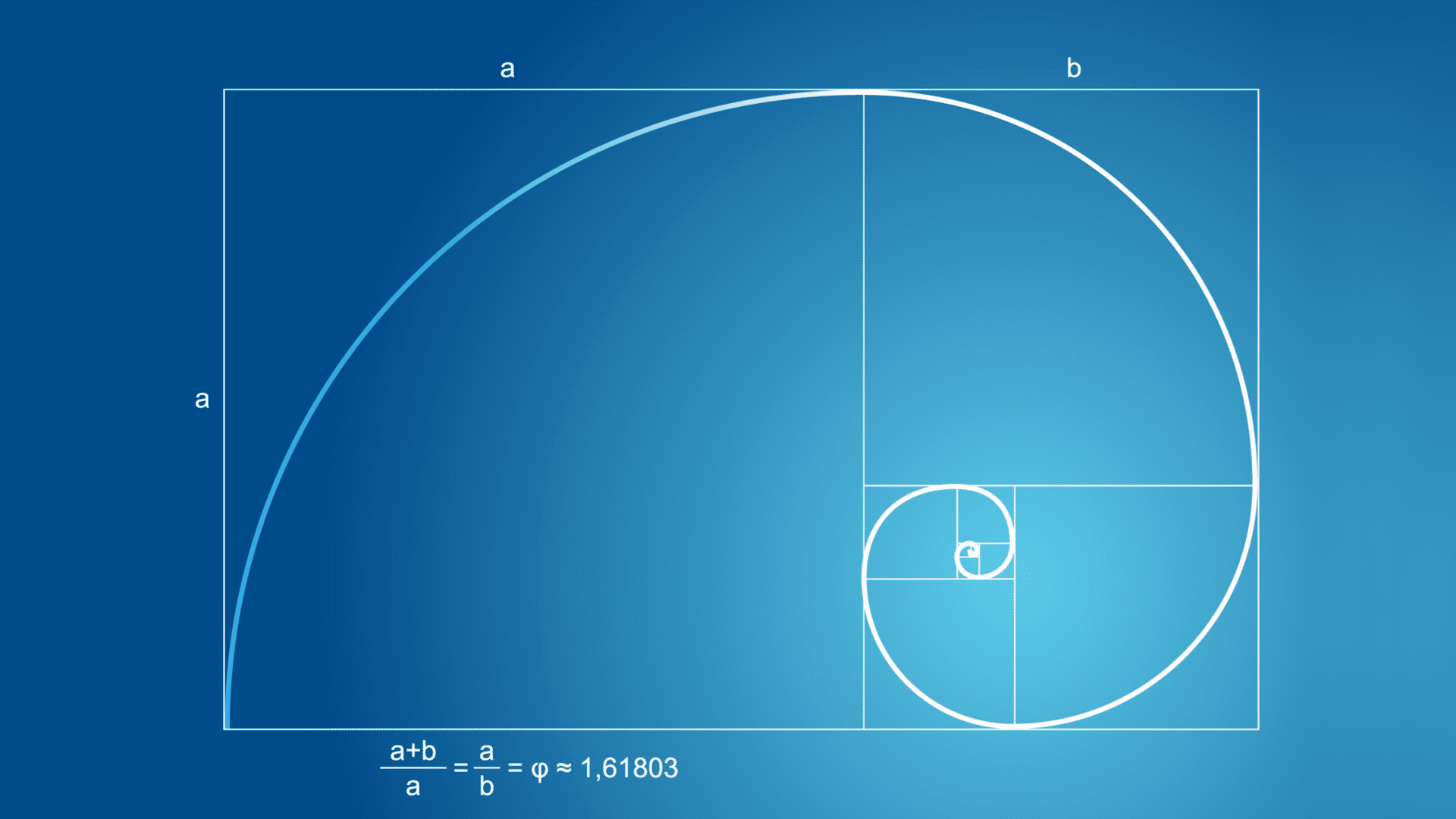
What Is Fibonacci Retracement? Leonardo Piscano was an Italian mathematician from Pisa. He was nicknamed Fibonacci and he found an interesting pattern in a certain set of numbers. That pattern or sequence is known as the Fibonacci sequence. In the Fibonacci sequence of numbers, after 0 and 1, each number is the sum of the … Read more