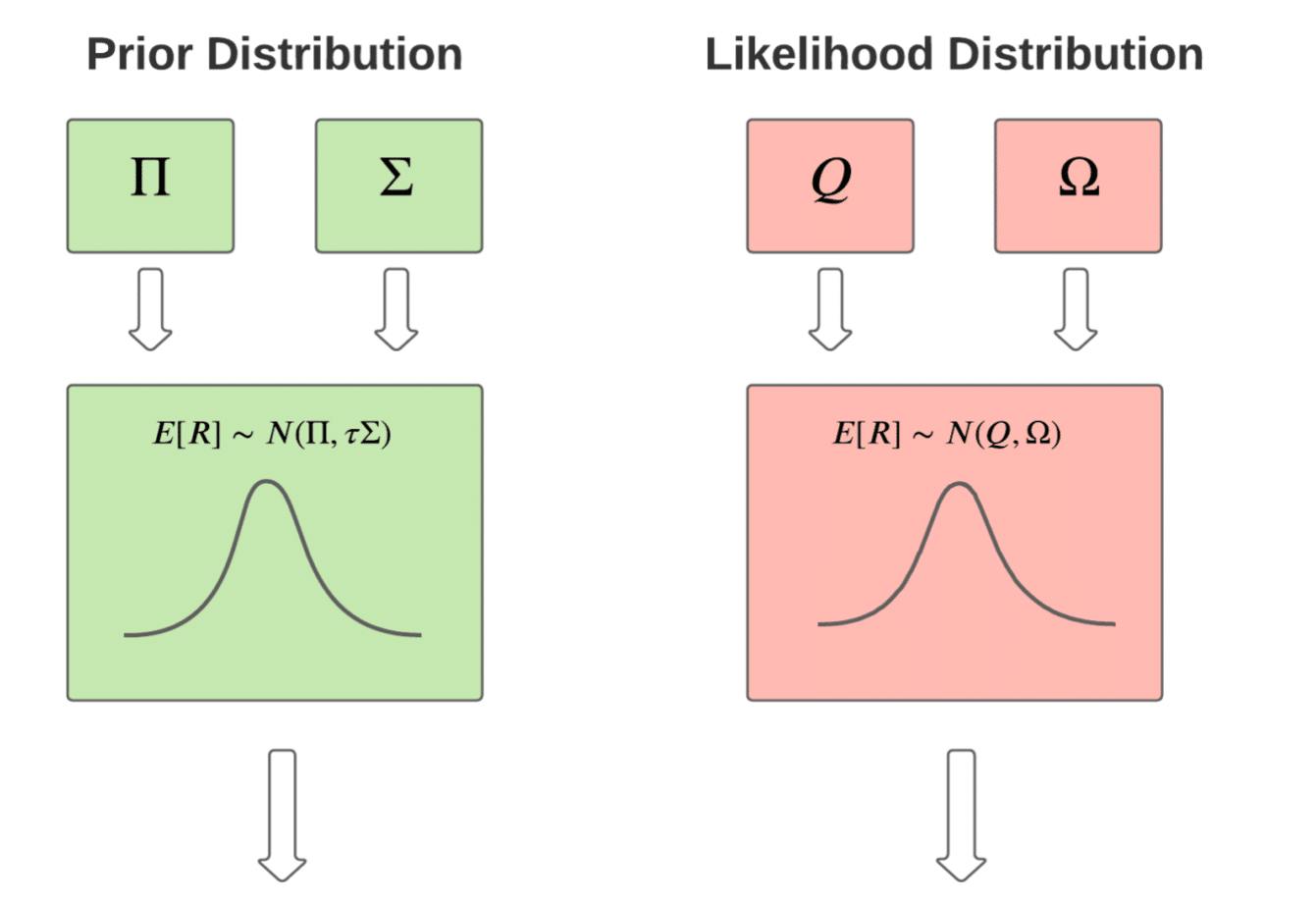
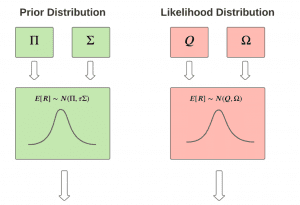
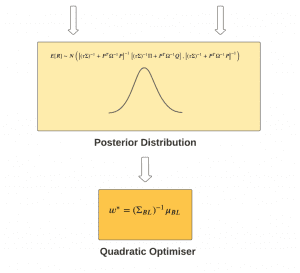
The Black-Litterman Model is a mathematical model used for portfolio allocation and optimisation. It is mainly used by portfolio managers of large investors, like insurance companies and mutual funds, to allocate their resources in various investments and assets. It was developed by Fischer Black and Robert Litterman of Goldman Sachs in 1990.
The BL model combines the Capital Asset Pricing Theory (CAPM) with Bayesian Statistics and the Modern Portfolio Theory to produce efficient estimates of portfolio weights.
Understanding the Modern Portfolio Theory
The modern portfolio theory is a theory on how risk-averse investors can construct portfolios to maximise the expected returns based on a given market risk level. It emphasises that the investor’s risk and returns are not independent observations, but they together influence the portfolio’s overall risk and return. The MPT talks about how investors can construct a diversified portfolio with multiple assets and maximise their returns for a given risk level.
However, the MPT is limited because it can only take into account the available historical market data, and then it uses the same to make assumptions about the future returns.
On the other hand, the Black-Litterman model lets the investor decide upon and apply their own views and risk preferences, and then it optimizes the asset allocation. The BL model improves the asset allocations provided by the MPT by incorporating projections on the future outlook and using pricing models that rely on subjective inputs in addition to objective inputs. However, there is a risk associated with incorporating subjective data as it may result in a biased model. For example, an overly optimistic view of one particular type of asset at a certain point in time may lead to portfolio managers assigning it a higher weight than what the MPT would recommend. If the asset then fails to keep up that momentum, it can result in significant losses, sometimes amounting to hundreds of billions of dollars.
Structure of the Black-Litterman Model
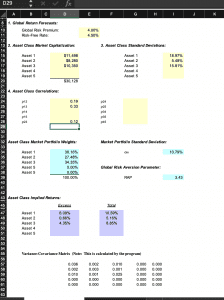
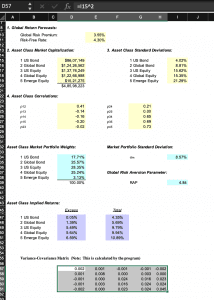
Let us consider a five-asset portfolio model and calculate the expected returns using the Black Litterman model. The user inputs data regarding the (i)global risk premium and risk-free rate, (ii) asset class market capitalisations, (iii) asset class standard deviations, and (iv) asset class correlation. Here we see the results for some sample data using the BL model formulae:
Limitations of the model
- Assumption of Normality
It is necessary to assume a normal distribution of the market returns. This assumption, in turn, makes the model constrained and reduces its flexibility to adapt to market parameters accurately.
- Limitations of the market portfolio
The calculations involved in the model rely heavily on the equilibrium portfolio, so any changes in the market portfolio affect the final BL weights. Market equilibrium is tough to define in practice because many risky assets are not taken into account. Thus it is challenging to accurately reproduce the optimal BL allocations using an imperfect market portfolio in the real world.
- Sensitivity to investor inputs
All portfolio models are affected by the investor’s input data, but the Black-Litterman model is especially sensitive because it contains the added parameter of investor beliefs. The investor has to be careful while trying to input their views into the model because that can easily sway the model’s predictions.
The Bottom Line
The Black-Litterman Model is a robust portfolio allocation algorithm that has broad uses in the finance industry. Despite its mathematical complexity, it simply combines Bayes Rule with the prior, current, and future data and expectations to formulate an optimal portfolio.
One of the Black-Litterman Model’s main advantages is that it allows investors and analysts to incorporate their own beliefs and opinions about the market into the calculations. This makes the BL model robust and reduces its sensitivity to the market dynamics and allows it to efficiently handle the variances of these views.
Disclaimer
None of the content published on marketxls.com constitutes a recommendation that any particular security, portfolio of securities, transaction, or investment strategy is suitable for any specific person. The author is not offering any professional advice of any kind. The reader should consult a professional financial advisor to determine their suitability for any strategies discussed herein. The article is written for helping users collect the required information from various sources deemed to be an authority in their content. The trademarks if any are the property of their owners and no representations are made.
References
faculty.mccombs.utexas.edu › ChileMaterial › Bla…